并查集

来自NOCOW

跳转到：导航, 搜索

[编辑] 什么是并查集？

并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。进行快速规整。

[编辑] 并查集的主要操作

合并两个不相交集合
判断两个元素是否属于同一集合

== 主要操作的解释及代码

需要注意的是，一开始我们假设元素都是分别属于一个独立的集合里的。

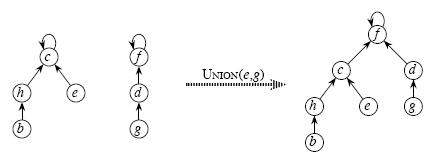
（1）合并两个不相交集合操作很简单：先设置一个数组Father[x]，表示x的“父亲”的编号。那么，合并两个不相交集合的方法就是，找到其中一个集合最父亲的父亲（也就是最久远的祖先），将另外一个集合的最久远的祖先的父亲指向它。

附图一张（摘自CLRS）——Ronice

a图为两个不相交集合，b图为合并后Father(b):=Father(g)

代码(pascal)：

Procedure Union(x,y:integer);{其中GetFather是下面将讲到的操作}
 var fx,fy : integer;
  begin
     fx := GetFather(x);
     fy := GetFather(y);
     if fx<>fy then Father[fx] := fy;{指向最祖先的祖先}
  end;

C：

inline void union(int x, int y)
{
    // get_father 是下面将讲到的操作
    father[get_father(x)] = get_father(y); //指向最祖先的祖先
}

（2）判断两个元素是否属于同一集合仍然使用上面的数组。则本操作即可转换为寻找两个元素的最久远祖先是否相同。可以采用递归实现。（有待补图，制作中）代码(pascal)：

Function Same(x,y:integer):boolean;
begin
  Same:=(GetFather(x)=GetFather(y));
end;

C:

inline char is_same(int x, int y)
{
    return get_father(x) == get_father(y);
}

[编辑] 并查集的优化

（1）路径压缩

刚才我们说过，寻找祖先时采用递归，但是一旦元素一多起来，或退化成一条链，每次GetFather都将会使用O（n）的复杂度，这显然不是我们想要的。

对此，我们必须要进行路径压缩，即我们找到最久远的祖先时“顺便”把它的子孙直接连接到它上面。这就是路径压缩了。使用路径压缩的代码如下，时间复杂度基本可以认为是常数的。

附图摘自CLRS：

pascal:

Procedure Initialize;
var
  i:integer;
begin
  for i:=1 to maxv do 
    Father[i]:=i;
end;

Function GetFather(v:integer):integer;
begin
  if Father[v]<>v then 
    Father[v]:=GetFather(Father[v]);
  exit(Father[v]);
end;

C:

void init(void)
{
    int i;
    for (i=0; i<MAX; i++)
        father[i] = i;
}

int get_father(int v)
{
    if (father[v] != v)
        father[v] = get_father(father[v]);
    return father[v];
}

（2）rank合并

合并时将元素少的集合合并到元素多的集合中。 pascal:

{ 初始化：fillchar(rank,sizeof(rank),0); }
function judge(x,y:integer):boolean;
 var fx,fy : integer;
  begin
     fx := GetFather(x);
     fy := GetFather(y);
     If fx=fy then exit(true) 
         else judge := false;
     if rank[fx]>rank[fy] then father[fy] := fx 
         else 
             begin
               father[fx] := fy;
               if rank[fx]=rank[fy] then inc(rank[fy]);
             end;
  end;

C:

// 初始化
static int rank[MAX] = { 0 };
 
char judge(int x, int y)
{
    int fx, fy;
    if ((fx = get_father(x)) == (fy = get_father(y)))
        return 1;
 
    if (rank[fx] > rank[fy])
        father[fy] = fx;
    else {
        father[fx] = fy;
        if (rank[fx] == rank[fy])
            rank[fy]++;
    }
    return 0;
}

[编辑] 时间复杂度

O(n*α(n))

其中α(x),对于x=宇宙中原子数之和,α(x)不大于4

事实上，路经压缩后的并查集的复杂度是一个很小的常数。

[编辑] 源代码

加了所有优化的代码框架：

pascal

c

c++(不含秩的优化)

[编辑] 习题

Noi2002 银河英雄传说

CEOI’99 Parity

Kruskal算法的优化

并查集

目录