Binary Indexed Tree

来自NOCOW

Binary Indexed Tree(树状数组)是一种树型数据结构，用于动态维护一个序列的前缀和。在实践中，它几乎总是用数组来实现；另外，由于代码易于记忆，它的树型结构很容易被忽略掉。它的中文名称“树状数组”很可能是因为以上两个特点得来。

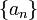
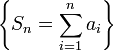
$\left\{ a_n \right\}$ $\left\{ S_n = \sum_{i=1}^n a_i \right\}$

[编辑] 结构

用C[i]表示从数据数组a中某一处一直到a[i]共2^k个元素的总和即a[i-2^k+1]~a[i] 而2^K就是i的二进制表示中倒数第一个1以及之后的0（比如(1001000)2的2^k就是(1000)=8）文件:BIT.jpg

LowBit，即2进制数中从最低位开始连续0的位数的关于2的幂，其值LowBit(x)=x∧-x（x&-x，x and -x）。也就是上文所说的2^k

LowBit(x)显然就是not x中最低的是0的那一位，(not x)+1的那一位则会变成1，其更低的位全部变成0，而更高的位不变。由于更高的位就是原数取反，和原数求and的值为0，最低位就是唯一的是1的位了。所以LowBit(x)=x and((not x)+1)。

举例说明：在x=10101000时，

not x=01010111
(not x)+1=01011000

和原数求and就是1000。

同时not x=-x-1，所以LowBit(x)=x and (-x)。

如果我们修改了a[i]，我们只需对c[i],c[i+lowbit(i)],c[i+lowbit(i)+lowbit(i+lowbit(i))]……进行修改，复杂度O(logn)

这种方式等效于每次在i的二进制末尾加0，达到跳到下一个区间节点的目的

pascal代码:

procedure modify(x,delta:longint);
  begin
    while x<=n do
      begin
        inc(c[x],delta);
        inc(x,lowbit(x));
      end;
  end;

a[1]+...+a[i]=c[i]+c[i-lowbit(i)]+c[i-lowbit(i)-lowbit(i-lowbit(i))]……复杂度O(logn)

这种处理方式等效与每次将i二进制的1末尾删去一个1，那么就刚好跳出这个i管辖的区间而达到分段计值的目的

pascal代码:

function sum(x:longint):longint;
  begin
    sum:=0;
    while x>0 do
      begin
        inc(sum,c[x]);
        dec(x,lowbit(x));
      end;
  end;

查询a[i]...a[j],则可调用sum(j)-sum(i-1)

*我要推广它的English Name.--Exile 15:52 2007年8月8日 (CST)

why? --Cosechy 14:53 2007年8月13日 (CST)

Binary Indexed Tree是一个小作品，欢迎帮助扩充这个条目。